Multi Arm Bandit Problem¶
Introduction¶
Row of slot machines with different probabilities of paying off? Which ones should you play often and how often?
Exploit vs Explore
Application Areas
Model for A/B Testing: Ad someone clicks or doesnot
Medical Diagnosis: Well known treatment or new treatment
Diseases Epidemic :
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import seaborn as sns
import empiricaldist
from empiricaldist import Pmf, Distribution
from ipywidgets import interact, interactive, fixed
Prior¶
def decorate_bandit(title):
"""
Labels the axes
title: string
"""
plt.xlabel('Probability of winning')
plt.ylabel('PMF')
plt.title(title)
bandit = Pmf.from_seq(range(101))
bandit.plot()
decorate_bandit(title="Prior Distribution")
We are assuming uniform prior distribution here for probability
def likelihood_bandit(data, hypo):
x = hypo/100
if data == "W":
return x
else:
return 1-x
actual_probs = [0.1, 0.2, 0.3, 0.4]
def posterior(n_w=1, n_l=9):
bandit = Pmf.from_seq(range(101))
outcomes = 'W'*n_w+"L"*n_l
bandit.plot(color='steelblue', label='Prior', linestyle="--")
for data in outcomes:
bandit.update(likelihood_bandit, data)
bandit.plot(color='steelblue', label='Posterior')
plt.legend()
decorate_bandit(title="Prior vs Posterior")
interactive(posterior, n_w=(0,10), n_l=(0,10))
Simulate Machines Based on Given Probabilities¶
from random import random
from collections import Counter
counter = Counter()
def flip(p):
return random()<p
def play(i):
counter[i] += 1
p = actual_probs[i]
if flip(p):
return 'W'
else:
return 'L'
play(1), play(2), play(3), play(0)
('W', 'L', 'W', 'W')
Playing machines 20 times¶
results = []
for i in range(20):
single = []
for j in range(4):
# print(i,j)
single.append(play(j))
results.append(single)
counter[4]
0
list(range(4))
[0, 1, 2, 3]
results
[['L', 'L', 'L', 'L'],
['L', 'W', 'L', 'W'],
['L', 'W', 'L', 'L'],
['L', 'W', 'W', 'L'],
['L', 'W', 'L', 'W'],
['L', 'L', 'L', 'L'],
['L', 'L', 'W', 'L'],
['L', 'W', 'W', 'L'],
['L', 'L', 'L', 'W'],
['W', 'W', 'L', 'L'],
['L', 'L', 'L', 'L'],
['L', 'L', 'W', 'L'],
['W', 'W', 'W', 'L'],
['L', 'W', 'L', 'L'],
['L', 'W', 'W', 'W'],
['L', 'W', 'L', 'W'],
['L', 'W', 'W', 'L'],
['W', 'L', 'L', 'L'],
['L', 'L', 'L', 'L'],
['L', 'L', 'L', 'L']]
prior = range(101)
beliefs = [Pmf.from_seq(prior) for i in range(4)]
beliefs
[0 0.009901
1 0.009901
2 0.009901
3 0.009901
4 0.009901
...
96 0.009901
97 0.009901
98 0.009901
99 0.009901
100 0.009901
Length: 101, dtype: float64,
0 0.009901
1 0.009901
2 0.009901
3 0.009901
4 0.009901
...
96 0.009901
97 0.009901
98 0.009901
99 0.009901
100 0.009901
Length: 101, dtype: float64,
0 0.009901
1 0.009901
2 0.009901
3 0.009901
4 0.009901
...
96 0.009901
97 0.009901
98 0.009901
99 0.009901
100 0.009901
Length: 101, dtype: float64,
0 0.009901
1 0.009901
2 0.009901
3 0.009901
4 0.009901
...
96 0.009901
97 0.009901
98 0.009901
99 0.009901
100 0.009901
Length: 101, dtype: float64]
options = dict(xticklabels='invisible', yticklabels='invisible')
def plot(beliefs,label_pre='Prior',**options):
sns.set_context('paper')
for i, b in enumerate(beliefs):
plt.subplot(2,2, i+1, label=f"{label_pre}{i}")
b.plot(label=f"Machine {i}")
plt.gca().set_yticklabels([])
plt.legend()
plt.tight_layout()
sns.set_context('talk')
plot(beliefs)
def update(beliefs, i, outcome):
beliefs[i].update(likelihood_bandit, outcome)
prior = range(101)
counter = Counter()
def flip(p):
return random()<p
def play(i):
counter[i] += 1
p = actual_probs[i]
if flip(p):
return 'W'
else:
return 'L'
def update(beliefs, i, outcome):
beliefs[i].update(likelihood_bandit, outcome)
beliefs = [Pmf.from_seq(prior) for i in range(4)]
# beliefs
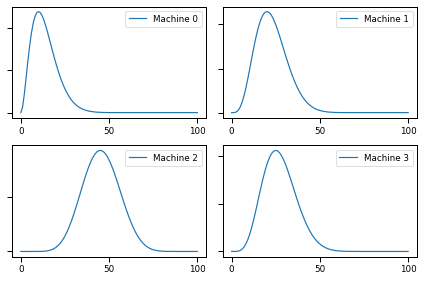
plot(beliefs, label_pre='Prior')
for i in range(20):
for j in range(4):
update(beliefs, j, play(j))
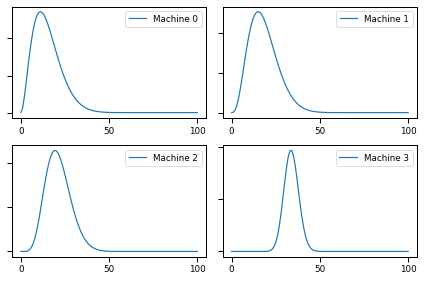
plot(beliefs, label_pre='Posterior')
for i, b in enumerate(beliefs):
print(f"{b.mean():0.02f}", b.credible_interval(0.9))
9.12 [ 2. 21.]
22.73 [10. 38.]
50.00 [33. 67.]
27.27 [13. 44.]
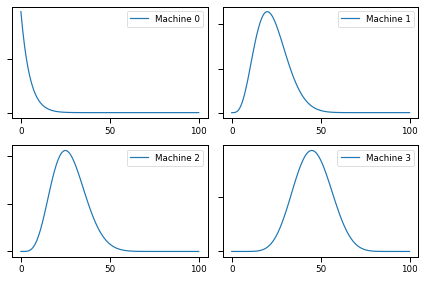
Bayesian Bandit¶
Idea is to choose best course of action while running the experiment/ simulation
Choice internally call np.random.choice on quantities
# def choose(beliefs):
# ps = []
beliefs[3].choice()
40
# Pmf.choice?
beliefs[3].qs
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,
13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25,
26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38,
39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51,
52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64,
65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77,
78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90,
91, 92, 93, 94, 95, 96, 97, 98, 99, 100])
ps = [b.choice() for b in beliefs]
ps, np.argmax(ps)
([0, 11, 21, 40], 3)
def choose(beliefs):
ps = [b.choice() for b in beliefs]
return np.argmax(ps)
choose(beliefs)
3
def choose_play_update(beliefs, verbose=False):
machine = choose(beliefs)
outcome = play(machine)
update(beliefs,machine,outcome)
if verbose:
print(machine, outcome, beliefs[machine].mean())
choose_play_update(beliefs, verbose=True)
3 W 42.85714285714286
prior = range(101)
beliefs = [Pmf.from_seq(prior) for i in range(4)]
counter = Counter()
num_plays = 200
for i in range(num_plays):
choose_play_update(beliefs)
plot(beliefs)
for i,b in enumerate(beliefs):
print(b.mean(), b.credible_interval(0.9))
15.000082130288831 [ 4. 30.]
18.181782304462693 [ 7. 33.]
21.2121212181695 [11. 34.]
33.834586466165426 [27. 41.]
for machine, count in sorted(counter.items()):
print(machine , count)
0 18
1 20
2 31
3 131